Lidar Data Fix for Complex Terrain
Lidar devices are being used more and more to conduct wind resource assessment, as an alternative to meteorological masts. This is because they have several advantages over the traditional measuring technology. Once a meteorological mast is installed, both the position and height of conventional anemometers are fixed, therefore limiting the measurements to certain locations and heights; Lidars easily overcome this inconvenience with their inherent portability. Lidars can also measure wind speeds at greater heights than most meteorological masts. Given increasing onshore wind turbine heights - and rotor diameters reaching upwards of 525 feet (160 meters) - this ability is crucial.
Ground-based, vertically-scanning Lidars calculate the wind speed based on measurements performed on a circular scanned area (as seen in Figure 1). The Lidar measures
and
. This area has a diameter size close to the size of the measured height.
.png)
Figure 1
The calculation for the wind speed assumes that the flow over the measurement circle is homogeneous, and therefore that
and consequently that
. However, this assumption breaks down when the flow is non-uniform, which is typical for a non-simple terrain. What is desired is the corrected wind speed
.
According to Sanquer et al. (Sanquer & Woodward, 2016) the general equation for is:
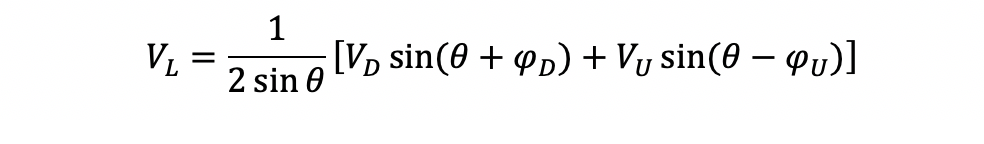
Therefore, ,
,
,
and
must be obtained.
is easily obtained: it is simply the half cone scan angle of the specific Lidar being used. On the other hand, an accurate wind flow model is required to obtain both the wind speeds (
and
)and the inflow angles (
and
).
Therefore, the correction factor is:
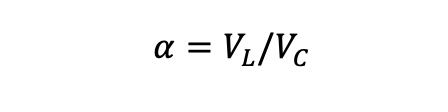
For the accurate acquirement of wind speeds and inflow angles, flow features typical of non-simple terrain, such as separation and recirculation, must be modeled accurately. Using a wind flow model such as Computational Fluid Dynamics (CFD), it is possible to compute the set of factors so that the correction of Lidar result data is similar to what's measured by a conventional anemometer at the point of interest, directly above the measuring device (Bingöl, Mann, & Foussekis, 2009).
Sanquer et al. (Sanquer & Woodward, 2016) used CFD to solve the Reynolds Averaged Navier-Stokes (RANS) equations to compute the required wind speeds and inflow angles. This method solves the RANS equations in a refined mesh around the Lidar location, hence obtaining the wind speeds and inflow angles at the desired locations.
Non-simple terrains will induce flow distortion, causing to be different than
. This makes it extremely important to determine which types of terrain are not simple ones.
.jpg)
The complexity of terrain may be determined by using the ruggedness index, as described by both Berge et al. (Berge, Nyhammer, Tallhaug, & Jacobsen, 2006) and Bowen et al. (Bowen & Mortensen, 1996). The ruggedness index is defined as the fractional area of a terrain in the circular vicinity of a point of interest which exceeds a critical slope. However, applying the ruggedness index means having to select the critical slope; additionally, forest influences on the wind flow are not considered. The relationship between WAsP prediction errors and site ruggedness has been explored by Mortensen et al. (Mortensen, Tindal, & Landberg, 2008). Taking into account these references, it is best to follow Bingöl (Bingöl F. , 2010), which proposes a classification for the complexity of a site based on the following categories:
- Flat terrain
- Moderately complex terrain (hilly or vegetated)
- Complex terrain (mountains or forests)
- Highly complex terrain (any combination of moderately complex and complex site characteristics)
Sanquer et al. (Sanquer & Woodward, 2016) tested this method on eight different sites of varying complexity. The results of that testing concluded that applying the CFD correction to data from Lidars in complex terrain improves the agreement between wind speed measurements from Lidars and meteorological masts. Additionally, for moderately complex terrain and complex terrain, the CFD correction of Lidar result data should be a standard process.
Juan Camilo Daza is a Business Development Engineer for Meteodyn, a numerical engineering and climatology company dedicated to the sectors of renewable energy, wind simulation, meteorology, and wind safety.
Meteodyn | meteodyn.com
References
Berge, E., Nyhammer, F., Tallhaug, L., & Jacobsen, Ø. (2006). An Evaluation of the WAsP Model at a Coastal Mountainous Site in Norway. Wind Energy, 9, 131 - 140.
Bingöl, F. (2010). Complex Terrain and Wind Lidars. Risø National Laboratory for Sustainable Energy.
Bingöl, F., Mann, J., & Foussekis, D. (2009). Conically scanning lidar error in complex terrain. Meteorologische Zeitschrift, 18(2), 189 - 195.
Bowen, A., & Mortensen, N. (1996). Exploring the limits of WAsP: the wind Atlas Analysis and application program. European Union Wind Energy Conference.
Mortensen, N., Tindal, A., & Landberg, L. (2008). Field validation of the RIX performance indicator for flow in complex terrain. EWEA Conference.
Sanquer, S., & Woodward, A. (2016). Post conversion of Lidar data on complex terrains.
Author: Juan Camilo Daza
Volume: 2021 January/February









